On July 28, 1945, a ten-ton (10,000 kg) B-25 bomber crashed into the Empire State Building at an estimated 400 kph, into the north face of the 79th floor. Although several people were killed, the building remained standing (Levy and Salvadori, 1992).
To estimate the force applied to the building, we must estimate either the deceleration of the bomber as it crashed into the building (and use the force-acceleration method), estimate the distance it took the bomber to come to rest (and use work-energy), or estimate the time it took to bomber to come to rest (and use impulse-momentum). The bomber did not pass through the building, so a distance of 10 to 20 meters for the plane to come to rest could be used for calculations. If the bomber came to rest in 20 meters with a constant deceleration, the force would be about 4440 kilonewtons exerted over about 0.25 seconds.
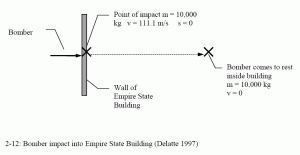
All three of these methods are derived from F = ma. The acceleration is assumed to be constant and is integrated once for velocity and twice for distance traveled. This problem is useful for demonstrating the equivalence of the three methods.
This case study was originally written in 1997 (Delatte, 1997), well before the terrorist attacks of September 11, 2001 (see World Trade Center and Pentagon). The same methods may be applied to calculate the impact forces applied by any aircraft of known weight and speed, with an estimate of the average distance before the aircraft (or its parts) came to rest.
Reference: Levy and Salvadori, 1992.





